I found some very old code with some immutable AVL & Red-Black tree implementations, so I figured I’d share. To begin with, let’s define some common functions across both data structures. We could use protocols, but our implementations are going to be extremely lightweight, both defined over vectors of the shape [left-child right-child key value …].
(ns trees.common
(:refer-clojure :exclude [key val find]))
(def left first)
(def right second)
(defn key [node] (nth node 2))
(defn val [node] (nth node 3))
(defn find [node k]
(when node
(let [cmp (compare k (key node))]
(cond (zero? cmp) (val node)
(neg? cmp) (recur (left node) k)
:else (recur (right node) k)))))
Let’s start with an AVL tree. We’re going to be really lazy and not store the node height inside the nodes, as this’d require some bookkeeping, but rather recalculate it on re-balance.
(ns trees.avl
(:require [trees.common :refer [key val find]])
(:refer-clojure :exclude [key val find]))
(defn- height
([tree] (height tree 0))
([tree n]
(if tree
(max (height (left tree) (inc n))
(height (right tree) (inc n)))
n)))
(defn- tilt [n]
(- (height (left n)) (height (right n))))
(defn avl-node [l r k v]
[l r k v])
(defn- rotate-l [[l r k v]]
(let [l (avl-node l (left r) k v)]
(avl-node l (right r) (key r) (val r))))
(defn- rotate-r [[l r k v]]
(let [r (avl-node (right l) r k v)]
(avl-node (left l) r (key l) (val l))))
(defn- balance [[l r k v :as node]]
(cond
(< 1 (tilt node)) (rotate-r
(if (neg? (tilt l))
(avl-node (rotate-l l) r k v)
node))
(< (tilt node) -1) (rotate-l
(if (pos? (tilt r))
(avl-node l (rotate-r r) k v)
node))
:else node))
(defn add [node k' v']
(if-let [[l r k v] node]
(let [cmp (compare k' k)]
(if (zero? cmp)
(avl-node l r k v')
(balance
(if (neg? cmp)
(avl-node (add l k' v') r k v)
(avl-node l (add r k' v') k v)))))
(avl-node nil nil k' v')))
Part of what keeps it succint is that all of the functions (left, right, add, etc.) are nil-safe. And also that we can’t remove anything. Let’s try something to see if it works!
trees.avl> (let [m (zipmap (shuffle (map str "abcdedfgh")) (range))]
(def tree (reduce-kv add nil m)))
trees.avl> (require '[rhizome.viz :refer [view-tree]])
trees.avl> (view-tree
identity
#(filter identity [(left %) (right %)])
tree
:node->descriptor (fn [x] {:label (key x)}))

Now let’s take a look at a very compact Red-Black tree implementation. As far as I can recall, I followed the strategy outlined here, where perfectly balanced trees are permitted to be all black. core.match makes the balancing easy, if not a little hairy.
(ns trees.rb
(:require [clojure.core.match :refer [match]])
(:require [trees.common :refer [find key val]])
(:refer-clojure :exclude [find key val]))
(def color last)
(def red? (comp #{:R} color))
(defn balance [node]
(match [node]
[(:or [[[a b xk xv :R] c yk yv :R] d zk zv :B]
[[a [b c yk yv :R] xk xv :R] d zk zv :B]
[a [[b c yk yv :R] d zk zv :R] xk xv :B]
[a [b [c d zk zv :R] yk yv :R] xk xv :B])] ;; =>
[[a b xk xv :B] [c d zk zv :B] yk yv :R]
:else node))
(defn- add* [node k' v']
(if-let [[l r k v c] node]
(let [cmp (compare k' k)]
(if (zero? cmp)
[l r k v' c]
(balance
(if (neg? cmp)
[(add* l k' v') r k v c]
[l (add* r k' v') k v c]))))
[nil nil k' v' :R]))
(defn add [node k v]
(assoc (add* node k v) 4 :B))
We can view the same tree as above:
trees.rb> (view-tree
identity
#(filter identity [(left %) (right %)])
tree
:node->descriptor
(fn [x] (cond-> {:label (key x)}
(red? x) (assoc :color "red"))))
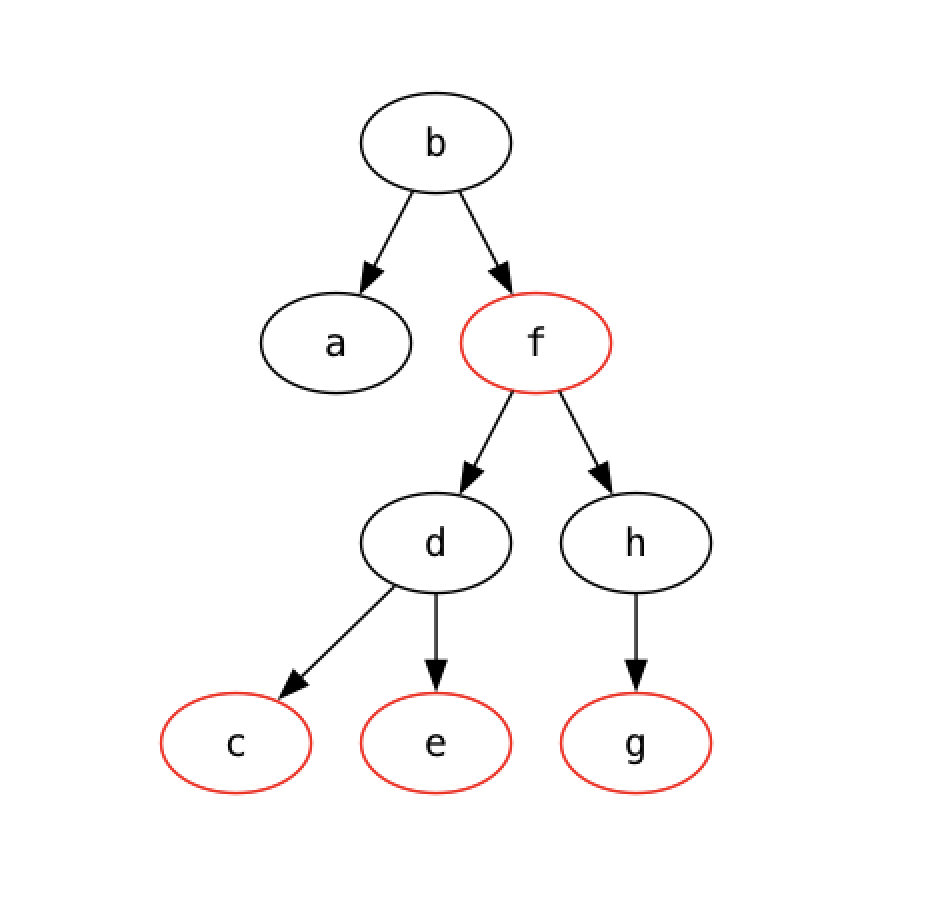
That’s about it for now. Let me know if I got anything horrendously wrong, like I said, it’s old code. It looks right!